Motivation
This blog is the second one of my 3 blogs about VAR model. In this blog, I will introduce how to use Stata’s integrated commands var and svar to estimate the VAR model, which is also the common practices for researchers in VAR estimation. While it has little incremental value to an extant blog Vector autoregressions in Stata written by David Schenck, this blog will serve as an important benchmark for my manual calculations of all the major VAR estimation outputs in the next blog.
Sample Dataset
The dataset used in this blog is a shipped dataset named varsample.dta. It can be accessed here. This dataset collects the quarterly times series of U.S. unemployment rate unrate, rate of consumer price inflation inflation, and short-term nominal interest rate (federal funds rate) ffr from 1968 to 2018.
1
2
3
4
5
6
7
8
9
10
11
12
|
. use varsample.dta, clear
. list in 1/5
+---------------------------------------------------------+
| n_date date ffr inflat~n unrate yq |
|---------------------------------------------------------|
1. | 1968-01-01 1968-01-01 4.5 -.659 3.7 32 |
2. | 1968-04-01 1968-04-01 5.5 -.656 3.5 33 |
3. | 1968-07-01 1968-07-01 6.13 -.651 3.7 34 |
4. | 1968-10-01 1968-10-01 6 -.647 3.4 35 |
5. | 1969-01-01 1969-01-01 4 -.643 3.4 36 |
+---------------------------------------------------------+
|
Set time series (tsset or xtset)
The prerequisite for var and svar is a well-defined consecutive time series. As the sample data is not panel data, I use tsset to do that. The consecutive quarterly time series variable in this dataset is yq.
1
2
3
4
|
. tsset yq
Time variable: yq, 32 to 235
Delta: 1 unit
|
Determine the time lag (varsoc)
I use varsoc command to run the lag-order selection. One can help varsoc to learn more details about the selection method. Both the likelihood ratio test and Akaike’s information criterion (AIC) recommend 7 lags, which I use through the rest of this post.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
. varsoc inflation unrate ffr, maxlag(8)
Lag-order selection criteria
Sample: 40 thru 235 Number of obs = 196
+---------------------------------------------------------------------------+
| Lag | LL LR df p FPE AIC HQIC SBIC |
|-----+---------------------------------------------------------------------|
| 0 | -1063.21 10.6553 10.8797 10.9 10.9299 |
| 1 | 170.566 2467.6 9 0.000 .00004 -1.61802 -1.53676 -1.41732 |
| 2 | 217.394 93.657 9 0.000 .000027 -2.00402 -1.86183 -1.6528 |
| 3 | 246.843 58.898 9 0.000 .000022 -2.21269 -2.00955* -1.71094* |
| 4 | 253.46 13.233 9 0.152 .000023 -2.18837 -1.92429 -1.53609 |
| 5 | 261.64 16.359 9 0.060 .000023 -2.18 -1.85498 -1.37719 |
| 6 | 273.936 24.593 9 0.003 .000022 -2.21363 -1.82768 -1.2603 |
| 7 | 285.311 22.751* 9 0.007 .000021* -2.23787* -1.79098 -1.13401 |
| 8 | 289.68 8.7374 9 0.462 .000023 -2.19061 -1.68278 -.936231 |
+---------------------------------------------------------------------------+
* optimal lag
Endogenous: inflation unrate ffr
Exogenous: _cons
|
Estimate the VAR system (var or svar)
Having decided that the 7 lags are appropriate for this VAR, we can use either var or svar command to estimate the coefficients of the VAR. Theoretically we need to decide whether the VAR system is stable before the VAR estimation but we can usually skip this step because the VAR estimation would not converge if the system were not stable.
var command
The var command and results are as follows.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
|
. var inflation unrate ffr, lags(1/7)
Vector autoregression
Sample: 39 thru 235 Number of obs = 197
Log likelihood = 288.0632 AIC = -2.254449
FPE = .0000211 HQIC = -1.809178
Det(Sigma_ml) = .0000108 SBIC = -1.154492
Equation Parms RMSE R-sq chi2 P>chi2
----------------------------------------------------------------
inflation 22 .008897 0.9998 1187611 0.0000
unrate 22 .283532 0.9710 6591.751 0.0000
ffr 22 1.64854 0.8694 1311.053 0.0000
----------------------------------------------------------------
------------------------------------------------------------------------------
| Coefficient Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
inflation |
inflation |
L1. | 1.16245 .0715051 16.26 0.000 1.022302 1.302597
L2. | -.384423 .1084028 -3.55 0.000 -.5968886 -.1719573
L3. | .3306758 .1089644 3.03 0.002 .1171096 .544242
L4. | -.1980314 .1101572 -1.80 0.072 -.4139356 .0178728
L5. | .2570946 .1089103 2.36 0.018 .0436344 .4705548
L6. | -.0861371 .1081372 -0.80 0.426 -.298082 .1258079
L7. | -.0796988 .0716629 -1.11 0.266 -.2201555 .060758
|
unrate |
L1. | -.0070429 .0023144 -3.04 0.002 -.0115791 -.0025067
L2. | .007192 .0037463 1.92 0.055 -.0001506 .0145345
L3. | .0021743 .0037601 0.58 0.563 -.0051954 .009544
L4. | .0024686 .0038336 0.64 0.520 -.0050451 .0099824
L5. | -.0096445 .0036164 -2.67 0.008 -.0167326 -.0025565
L6. | .0085564 .0037105 2.31 0.021 .001284 .0158289
L7. | -.0038481 .0022014 -1.75 0.080 -.0081629 .0004666
|
ffr |
L1. | .0000775 .000391 0.20 0.843 -.0006889 .0008439
L2. | .0009212 .0004199 2.19 0.028 .0000982 .0017442
L3. | .0007338 .0004222 1.74 0.082 -.0000936 .0015612
L4. | .0005146 .0004459 1.15 0.248 -.0003593 .0013884
L5. | -.0007561 .0004095 -1.85 0.065 -.0015587 .0000466
L6. | -.0002788 .0004089 -0.68 0.495 -.0010803 .0005227
L7. | -.0008528 .0003889 -2.19 0.028 -.0016149 -.0000906
|
_cons | .0070745 .0031262 2.26 0.024 .0009471 .0132018
-------------+----------------------------------------------------------------
unrate |
inflation |
L1. | -1.231156 2.278772 -0.54 0.589 -5.697468 3.235156
L2. | 3.443442 3.454654 1.00 0.319 -3.327556 10.21444
L3. | -.1066172 3.472549 -0.03 0.976 -6.912689 6.699454
L4. | 1.259347 3.510564 0.36 0.720 -5.621233 8.139927
L5. | -2.66152 3.470825 -0.77 0.443 -9.464212 4.141172
L6. | .8081638 3.446187 0.23 0.815 -5.946239 7.562567
L7. | -1.480169 2.283801 -0.65 0.517 -5.956338 2.995999
|
unrate |
L1. | 1.329821 .0737573 18.03 0.000 1.185259 1.474382
L2. | .0023896 .1193886 0.02 0.984 -.2316077 .2363869
L3. | -.3491413 .1198299 -2.91 0.004 -.5840036 -.1142791
L4. | -.1870338 .1221724 -1.53 0.126 -.4264873 .0524197
L5. | .2609972 .1152507 2.26 0.024 .0351099 .4868844
L6. | -.0892354 .1182482 -0.75 0.450 -.3209976 .1425267
L7. | -.0158381 .0701571 -0.23 0.821 -.1533434 .1216672
|
ffr |
L1. | .0391868 .0124618 3.14 0.002 .0147622 .0636114
L2. | .0133781 .0133815 1.00 0.317 -.0128492 .0396054
L3. | -.0020393 .0134537 -0.15 0.880 -.0284081 .0243295
L4. | -.042115 .0142089 -2.96 0.003 -.0699639 -.0142661
L5. | -.0104107 .0130509 -0.80 0.425 -.0359899 .0151686
L6. | -.0027428 .0130325 -0.21 0.833 -.028286 .0228003
L7. | .0179745 .0123927 1.45 0.147 -.0063148 .0422638
|
_cons | .1227788 .0996293 1.23 0.218 -.072491 .3180486
-------------+----------------------------------------------------------------
ffr |
inflation |
L1. | -4.707449 13.24949 -0.36 0.722 -30.67598 21.26108
L2. | 14.62629 20.08643 0.73 0.467 -24.7424 53.99498
L3. | -13.79702 20.19048 -0.68 0.494 -53.36964 25.7756
L4. | 18.50689 20.41152 0.91 0.365 -21.49894 58.51273
L5. | -8.194952 20.18046 -0.41 0.685 -47.74792 31.35802
L6. | 14.6829 20.03721 0.73 0.464 -24.5893 53.95511
L7. | -22.07114 13.27873 -1.66 0.096 -48.09697 3.954702
|
unrate |
L1. | -2.044818 .428848 -4.77 0.000 -2.885345 -1.204291
L2. | 1.542331 .6941623 2.22 0.026 .1817982 2.902864
L3. | .4599863 .6967282 0.66 0.509 -.9055759 1.825548
L4. | .2812749 .7103485 0.40 0.692 -1.110983 1.673532
L5. | .3858028 .6701035 0.58 0.565 -.9275758 1.699181
L6. | -1.11061 .6875317 -1.62 0.106 -2.458148 .2369271
L7. | .4463692 .4079151 1.09 0.274 -.3531296 1.245868
|
ffr |
L1. | .2870547 .0724567 3.96 0.000 .1450422 .4290672
L2. | .1779213 .0778042 2.29 0.022 .0254279 .3304148
L3. | .4496412 .0782241 5.75 0.000 .2963247 .6029577
L4. | .2517726 .0826149 3.05 0.002 .0898503 .4136949
L5. | .0537564 .0758819 0.71 0.479 -.0949694 .2024823
L6. | -.1680117 .0757748 -2.22 0.027 -.3165276 -.0194959
L7. | -.2284582 .0720552 -3.17 0.002 -.3696838 -.0872326
|
_cons | 1.077793 .5792758 1.86 0.063 -.057567 2.213152
------------------------------------------------------------------------------
|
svar command
One can find the precise specifications of this command in the handbook (p. 7) of Stata’s svar command (see in this link). The handbook also mentioned that one can manually add constraints to the SVAR model. In particular, one way to impose the Cholesky restrictions, which are by default used in the var command, is to specify the aeq and beq matrix as the following format.
$$
\mathbf{aeq}=\left[\begin{array}{lll}
1 & 0 & 0 \\\
\cdot & 1 & 0 \\\
\cdot & \cdot & 1
\end{array}\right] \quad \text { and } \quad \mathbf{beq}=\left[\begin{array}{ccc}
\cdot & 0 & 0 \\\
0 & . & 0 \\\
0 & 0 & \cdot
\end{array}\right]
$$
For me, the biggest incremental value of svar command to the var command is that it can automatically produce the estimation of the contemporaneous effects matrix A in the following structural-form VAR.
$$
Ax_t=\nu+\Sigma_{i=1}^{p}\Gamma_i x_{t-i}+e_t
$$
To be exact, the svar model stores the estimation of the matrix \(A\) in a matrix called e(A). With this matrix \(A\) , one can recover the structural shocks \(\epsilon_t\) and its covariance matrix \(\Sigma_\epsilon\) from reduced-form residuals \(e_t\) via \(\epsilon_t=Ae_t\) and \(\Sigma_\epsilon= A\Sigma_eA’\).
I skipped some details to be brief, readers who would like to dig deeper can find more details in Stata’s svar command handbook (see in this link). The svar command and results are as follows.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
|
. matrix A1 = (1,0,0 \ .,1,0 \ .,.,1)
. matrix B1 = (.,0,0 \ 0,.,0 \ 0,0,.)
. svar inflation unrate ffr, lags(1/7) aeq(A1) beq(B1)
Estimating short-run parameters
Iteration 0: log likelihood = -785.35924
Iteration 1: log likelihood = -217.78432
Iteration 2: log likelihood = 129.49698
Iteration 3: log likelihood = 277.75696
Iteration 4: log likelihood = 287.7111
Iteration 5: log likelihood = 288.06267
Iteration 6: log likelihood = 288.06322
Iteration 7: log likelihood = 288.06322
Structural vector autoregression
( 1) [/A]1_1 = 1
( 2) [/A]1_2 = 0
( 3) [/A]1_3 = 0
( 4) [/A]2_2 = 1
( 5) [/A]2_3 = 0
( 6) [/A]3_3 = 1
( 7) [/B]1_2 = 0
( 8) [/B]1_3 = 0
( 9) [/B]2_1 = 0
(10) [/B]2_3 = 0
(11) [/B]3_1 = 0
(12) [/B]3_2 = 0
Sample: 39 thru 235 Number of obs = 197
Exactly identified model Log likelihood = 288.0632
------------------------------------------------------------------------------
| Coefficient Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
/A |
1_1 | 1 (constrained)
2_1 | 2.838578 2.261524 1.26 0.209 -1.593927 7.271083
3_1 | -31.31379 12.54682 -2.50 0.013 -55.90511 -6.72248
1_2 | 0 (constrained)
2_2 | 1 (constrained)
3_2 | 1.510951 .3937039 3.84 0.000 .7393057 2.282597
1_3 | 0 (constrained)
2_3 | 0 (constrained)
3_3 | 1 (constrained)
-------------+----------------------------------------------------------------
/B |
1_1 | .0083854 .0004224 19.85 0.000 .0075574 .0092134
2_1 | 0 (constrained)
3_1 | 0 (constrained)
1_2 | 0 (constrained)
2_2 | .2661691 .0134094 19.85 0.000 .2398871 .292451
3_2 | 0 (constrained)
1_3 | 0 (constrained)
2_3 | 0 (constrained)
3_3 | 1.470823 .074099 19.85 0.000 1.325592 1.616055
------------------------------------------------------------------------------
. mat list e(A)
e(A)[3,3]
inflation unrate ffr
inflation 1 0 0
unrate 2.8385778 1 0
ffr -31.313794 1.5109512 1
|
If you’d like, you can list the reduced-form coefficients estimated by the above svar command, which are stored in a matrix named e(bf_var). Unsurprisingly, they are exactly the same as those estimated with var command.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
|
. mat list e(bf_var)
e(bf_var)[1,66]
inflation: inflation: inflation: inflation: inflation: inflation: inflation:
L. L2. L3. L4. L5. L6. L7.
inflation inflation inflation inflation inflation inflation inflation
r1 1.1624496 -.38442299 .33067581 -.19803137 .25709458 -.08613706 -.07969876
inflation: inflation: inflation: inflation: inflation: inflation: inflation:
L. L2. L3. L4. L5. L6. L7.
unrate unrate unrate unrate unrate unrate unrate
r1 -.00704289 .00719199 .00217432 .00246865 -.00964455 .00855645 -.00384815
inflation: inflation: inflation: inflation: inflation: inflation: inflation:
L. L2. L3. L4. L5. L6. L7.
ffr ffr ffr ffr ffr ffr ffr
r1 .0000775 .00092119 .00073382 .00051456 -.00075606 -.00027879 -.00085278
inflation: unrate: unrate: unrate: unrate: unrate: unrate:
L. L2. L3. L4. L5. L6.
_cons inflation inflation inflation inflation inflation inflation
r1 .00707448 -1.2311559 3.4434415 -.10661715 1.2593467 -2.6615204 .80816382
unrate: unrate: unrate: unrate: unrate: unrate: unrate:
L7. L. L2. L3. L4. L5. L6.
inflation unrate unrate unrate unrate unrate unrate
r1 -1.4801693 1.3298207 .00238958 -.34914135 -.18703379 .26099715 -.08923544
unrate: unrate: unrate: unrate: unrate: unrate: unrate:
L7. L. L2. L3. L4. L5. L6.
unrate ffr ffr ffr ffr ffr ffr
r1 -.0158381 .0391868 .0133781 -.0020393 -.04211502 -.01041068 -.00274284
unrate: unrate: ffr: ffr: ffr: ffr: ffr:
L7. L. L2. L3. L4. L5.
ffr _cons inflation inflation inflation inflation inflation
r1 .01797453 .12277881 -4.7074491 14.62629 -13.797021 18.506895 -8.1949518
ffr: ffr: ffr: ffr: ffr: ffr: ffr:
L6. L7. L. L2. L3. L4. L5.
inflation inflation unrate unrate unrate unrate unrate
r1 14.682903 -22.071136 -2.0448181 1.5423312 .45998626 .28127488 .38580282
ffr: ffr: ffr: ffr: ffr: ffr: ffr:
L6. L7. L. L2. L3. L4. L5.
unrate unrate ffr ffr ffr ffr ffr
r1 -1.1106103 .44636919 .28705469 .17792134 .44964119 .2517726 .05375644
ffr: ffr: ffr:
L6. L7.
ffr ffr _cons
r1 -.16801173 -.22845819 1.0777927
|
Obtain IRFs, OIRFs, and Variance Decomposition (irf create)
All the IRFs, OIRFs, and Variance Decomposition results can be conveniently obtained withirf create command. For example, the following command will create a file named myirf.irf to store the 15-step forward-looking impulse response functions (IRFs), orthogonalized IRFs (OIRFs), structural IRFs (SIRFs), cumulative IRFs (CIRFs), forecast-error variance decomposition (FEVD), etc. In this file, all these results are tagged to belong to the VAR estimation named forblog. You can change the parameters as you like following the syntax documented in this link.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
. irf create forblog, step(15) set(myirf) replace
(file myirf.irf created)
(file myirf.irf now active)
irfname forblog not found in myirf.irf
(file myirf.irf updated)
. preserve
. use myirf.irf, replace
. format *irf %6.0g
. list impulse response step irf cirf oirf sirf fevd in 19/27 ,noob
+------------------------------------------------------------------------------+
| impulse response step irf cirf oirf sirf fevd |
|------------------------------------------------------------------------------|
| inflation inflation 2 .9752 3.138 .0087 .0087 .9789 |
| unrate inflation 2 -.0105 -.0176 -.0031 -.0031 .02103 |
| ffr inflation 2 7.6e-04 8.4e-04 .0011 .0011 7.5e-05 |
| inflation unrate 2 .1906 -1.041 -.016 -.016 .00781 |
| unrate unrate 2 1.699 4.029 .4215 .4215 .97471 |
|------------------------------------------------------------------------------|
| ffr unrate 2 .0766 .1158 .1127 .1127 .01748 |
| inflation ffr 2 10.32 5.613 .1814 .1814 .03232 |
| unrate ffr 2 -1.731 -3.776 -.533 -.533 .19658 |
| ffr ffr 2 .1798 1.467 .2645 .2645 .7711 |
+------------------------------------------------------------------------------+
. restore
|
Visualization and Interpretation (irf table and irf graph)
You may visualize these outputs by listing tables or draw figures as you like.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
. irf graph oirf, impulse(inflation unrate ffr) response(inflation unrate ffr) yline(0,lcolor(black)) xlabel(0(5)15) byopts(yrescale)
. irf table oirf, impulse(inflation unrate ffr) response(inflation) noci
Results from forblog
-------------------------------------------
| (1) (2) (3)
Step | oirf oirf oirf
---------+---------------------------------
0 | .008385 0 0
1 | .009938 -.001906 .000114
2 | .008654 -.003105 .001114
3 | .009175 -.003778 .002361
4 | .009006 -.003715 .00351
5 | .009924 -.005065 .003886
6 | .011327 -.005197 .004351
7 | .011165 -.005552 .004475
8 | .011152 -.00589 .004739
9 | .011371 -.005636 .005334
10 | .011507 -.005857 .005339
11 | .011784 -.0058 .005251
12 | .011916 -.005575 .005234
13 | .011872 -.005392 .005132
14 | .011874 -.004973 .005162
15 | .011933 -.00466 .005074
-------------------------------------------
(1) irfname = forblog, impulse = inflation, and response = inflation.
(2) irfname = forblog, impulse = unrate, and response = inflation.
(3) irfname = forblog, impulse = ffr, and response = inflation.
|
The following graph displays the orthogonalized IRFs in the 15-step forward-looking timeframe. For each subfigure, there are three names in the head. They are the VAR estimation frame title, the impulse shock name, and the response equation name. Fort example, the figure in row 2 and column 3 displays the 15-step forward-looking response of unemployment rate (unrate) to the shock from inflation (inflation). It suggests that the unexpected shock from inflation triggers persistent elevated unemployment rate and this trend sustained over 15 quarters after the shock happened.
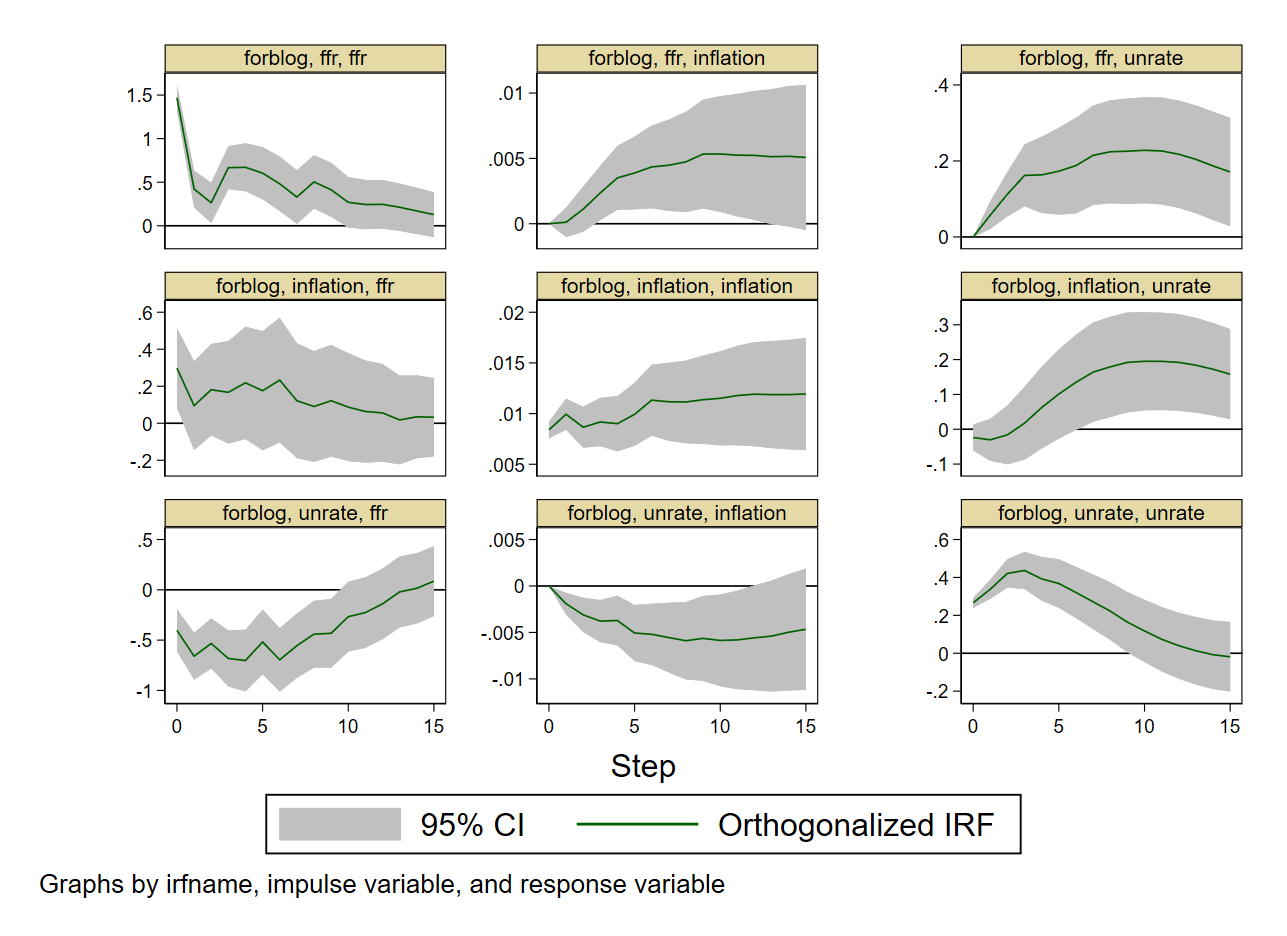
Figure 1: Graphs for Orthogonalized IRFs
Integrated Codes
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
* load data
sysuse varsample.dta, clear
* set time series
tsset yq
* choose lag orders
varsoc inflation unrate ffr, maxlag(8)
* estimate VAR using `var' command
var inflation unrate ffr, lags(1/7)
* estimate VAR using `svar' command
matrix A1 = (1,0,0 \ .,1,0 \ .,.,1)
matrix B1 = (.,0,0 \ 0,.,0 \ 0,0,.)
svar inflation unrate ffr, lags(1/7) aeq(A1) beq(B1)
* crete output dataset myirf.irf
irf create forblog, step(15) set(myirf) replace
* visualize irfs
irf graph oirf, impulse(inflation unrate ffr) response(inflation unrate ffr) yline(0,lcolor(black)) xlabel(0(5)15) byopts(yrescale)
irf table oirf, impulse(inflation unrate ffr) response(inflation) noci
|
Summary
In this blog, I show how to use the integrated order var and svar to produce stylized outputs of VAR estimation in Stata. They will be benchmarks for the next blog where I will manually replicate all these results in Stata to obtain deeper understanding about these outputs.
References
- Vector autoregressions in Stata by David Schenck
- Stata handbook on svar command
